題目：
　　　　　　　　

 

思考重點：可以直接算出、或嗎?

　　　　@.

　　　　　　　　　　

　　　　@.思考方向－－

　　　　　1圖中有好幾個三角形---利用外角定理，得

　　　　　2正方形邊長是平行線---想到平行線性質(內錯角相等、同側

　　　　　內角互補、同位角相等)，還是無法直接求出角度大小

　　　　　 如下圖

　　　　　　　　　　　　　　　　　　　　

　　　　@.大膽的猜測－－嗎？

　　　　　　　　　　

　　　　　　　　　　　　

　【作法一】國三程度的作法(利用相似形，證明)　　　　

　　　　
　　　　　則∠1+∠2+∠3 = 90°

 

　【作法二】國二程度的作法(利用畢氏定理，證明) 　　　　　　　　　很精彩的證法喔(謝謝 tseng同學提供)

　　　　１首先將的位置，轉換至下面來(最巧妙的一步)，如下圖。

　　　　２則ΔABC為一等腰直角三角形(WHY?)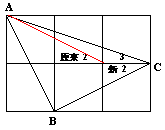

　　　　　∴∠2+∠3 ﹦45°

　　　　　即∠1+∠2+∠3 = 90°
　　　　

 

 

 

　【作法三】高一程度的作法(利用三角函數，證明)

　　　

　　　　則∠1+∠2+∠3 = 90°

 

 

 

　【作法四】高一程度的作法(利用三角函數，證明)

　　　

 

 

　【作法五】高一程度的作法(利用三角函數，證明∠1+∠2+∠3 = 90°)

　　　　

　　　　這個證明留給聰明的你去完成，有問題的話，請e-mail討論。

 

 

 

　　【推廣思考】

　　　　1.有沒有實驗方式的驗證法呢？(嚴格來說，只能當佐證)

　　　　　實驗１
　　　　　

　　　　　實驗２

　　　　　

　　　　　 　　　

　　　　2.你最喜歡那一種那一種證法?理由是什麼？

 

 

　【深層思考】
　　　　
　　　　１.如果正方形的數量是四個、五個、甚至以上，這些角度有規則

　　　　　可循嗎?

　　　　２.這個題目如果不是正方形，而是用三個長方形組合而成的，是否

　　　　　 有這種美妙的結論?

　　　　３.你想到了【作法二】的三角形，為什麼是直角三角形了嗎?
　　　　

　　　　４.你還有其他證法嗎？