問題
　　　小明投籃時，那個籃球的軌跡如下圖，請問你可以算出這個籃球會掉

在什麼地方嗎?

 

 

 

數學王子的話

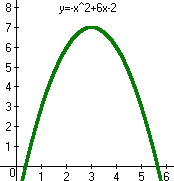
　　●十字交乘

　　　 　因為「因式展開」和「因式分解」就像一對雙胞胎兄弟一樣，所以

　　想了解因式分解中的十字交乘，就可以由「因式展開」看起。

　　
　　●觀察

　　【橫式乘法】
　　　(x+3)(x+5)=x+3x+5x+15=x+8x+15
　　　(x+y)(2x-y)=2x-xy+2xy-y= 2x+xy-y

　　【直式乘法】
　　　　　　(x+3)(x+5) 　　　　　(x+y)(2x-y)

　　　　
　　　　　x+8x+15 　　　　　　　2x+xy-y

　　◎小結論：在一個有一個未知數的二次三項中，十字交乘的方法是：

　　　二次項(x)： 未知數•未知數(x•x)　
　　　一次項(8x) ： 數字•x
　　　常數項(15) ： 數字•數字

　　●進行解題

　　　那麼x＋6x-2=(X+?)(X+?)，要如何利用十字交乘來因式分解呢?

　　　很抱歉，這一題是無法利用十字交乘來因式分解的，因為如果可以

　　作到的話，假設　x＋6x-2=(X+P)(X+Q)

　　　此處PQ=-2 , P+Q=6

　　　很明顯的，我們找不到適合的整數來符合上述的式子。　

　　　那麼究竟要如何作才能解出這一題呢?

　　　請參考下一個專題－－－配方法。

　　●深入思考

　　　　如果當我們要因式分解時，發現它的樣子形如:　　

　　１.x-xy-2y+x+7y-6，可以用上述十字交乘的觀念來因式分解嗎？

　　　答：可以，這時候就叫作「雙十字交乘」。

　　　　　
　　　　　　最後檢查x的係數是否正確?　　∵　3x-2x=x OK!

　　　　　所以，x-xy-2y+x+7y-6＝(x+y-2)(x-2y+3)

　　　　　【提醒】：你也可以只寫係數就好，這就叫稱為「分離係數」

　　２.練習：因式分解　x-6xy+9y+x-3y-20

　　　答：利用「雙十字交乘」　　
　　　　　　　　記得檢驗x的係數是否正確?!

　　　　　∴x-6xy+9y+x-3y-20＝(x-3y-4)(x-3y+5)

　　　　　另法：「乘法公式」＋「十字交乘」

　　　　　　　∵　x-6xy+9y＝(x-3y)

　　　　　　　∴　原式＝(x-3y)+(x-3y)-20

　　　　　　　　　再利用十字交乘，可得

　　　　　　　原式＝(x-3y-4)(x-3y+5)