數學王子的提醒
依照題意，我們可以這樣思考：
【法一：直接計算】
但是我們會發現這個交集部份，並不是我們熟悉的幾何圖形，
當然也就不知道，它有什麼面積公式可以應用。
【法二：貼貼補補法】
大家一定學過一些幾何圖形，也知道它們的面積的算法，所以
遇到這類型的題目時，我們就會儘量把它們拉上關係。
目標：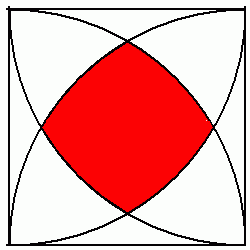
拉關係：
關鍵：利用大正方形面積－４個黑色部份面積
【如何算】
：利用１/４圓－
←這是一個弓形和一個60°扇形的組合
而弓形又要怎麼算呢？
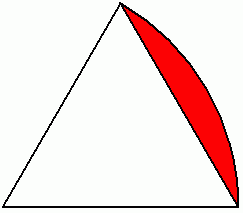
其實就是用一個60°扇形－正△的面積。
●開始計算：
正方形面積：1
一個60°扇形：60/360 ×1×1×π=1/6π
正△形面積：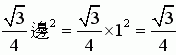
∴弓形面積＝1/6π－
因此＝一個60°扇形＋弓形
＝
1/6π＋1/6π－＝1/3π－
最後：＝1/4圓－
＝1/4π－1/3π＋
有４個黑色區域，所以＝
∴＝１－
小提醒
這一題可以學到好幾個基本平面圖形的面積算法，請
再思考、品味一下喔！
