注意!不是重疊喔，只是看起來像而已!

當我們學數學時，常常會被老師教我們的內容所限

　　　　制，例如１－１是畫二次函數的圖形，那麼，我

　　　　們只會在意二次函數，但是其他次方的函數，它

　　　　們的圖形會如何呢？讓我們叛逆一次，探索看看

　　　　吧！

 

　　　　見１－１的課前知識。

 

　　　　在1-1中提到一二次函數的圖形一定會是拋物線，

　　　　那麼如果不是二次函數，圖形又會是什麼樣子呢

　　　　？這是本單元探討的主題。

　　　　1.複習一次函數的圖形都是直線。

　　　　2.畫畫。

　　　　3.畫畫。　

　　　　4.畫畫。

　　　　5.你得到了什麼結論?

 

一次函數的圖形

　　　　１.請試著畫出以下的圖形：

　　　　　　

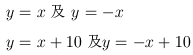
　　　　　【作法】在描點之後得：

　　　　　 　　　

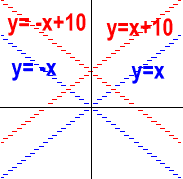
　　　　２.請試著畫出以下的圖形：

　　　　　　　

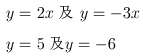
　　　　　【作法】在描點之後得：

　　　　　　　　　

　　　　

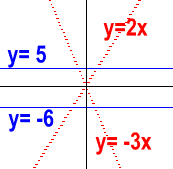
結論

　　　　１.由上例可知一次函數的解有無限多個(Why?)，

　　　　　且圖形為一直線，因此通常作圖只畫２個點。

　　　　２.若 y=ax+b，a不為０時，

　　　　【方向性】

　　　　　(1) a＞０往右上，a＜０往左上(a叫斜率)

　　　　　(2) a＝０水平線（平行y軸）

　　　　　(3) a、b均＝為０　＝＞　x軸　

　　　　　(4) 沒有常數項，必通過原點。

　　　　【平移特性】

　　　　　y=ax+b的圖形是 將y=ax的圖形　往上移b單位

　　　　　(註: 若b<0代表則往下移b單位)

 

三次函數(或三次以上)的圖形

　　　　１.請試著畫出以下的圖形：

　　　　　

　　　　　

　　　　　

　　　　　【作法】以為例，

　　　　　　　　　在描點之後得：

 

　

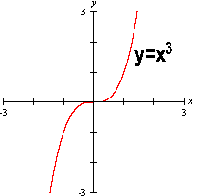
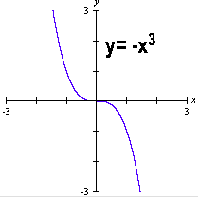
　　　　　　　如果將二次與三次畫在一起，則得

　　　　　　　　

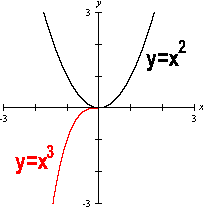
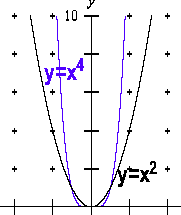
　　　　　　　如果將二次與四次畫在一起，則得

　　　　　　　　

　　　　　　　如果將三次與五次畫在一起，則得

　　　　　　　　

　　　　

　

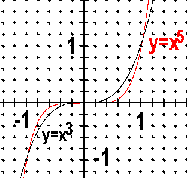
結論

　　　　１.由上例可知二次函數與四次函數的圖形較接近

　　　　　，而二次函數與四次函數的圖形較接近。

　　　　２.

　　　　【對稱性】

　　　　　(1) 二次函數與四次函數的圖形：線對稱

　　　　　(2) 三次函數與五次函數的圖形：點對稱

　　　　3.推論：

　　　　　偶次函數：(1)線對稱

　　　　　　　　　　(2)開口向上(有最小值)或向下(最大

　　　　　　　　　　　值)：由最高次係數決定。

　　　　　奇次函數：(1)點對稱

 

預定學習時間：

其他函數的圖形

進度 §

3

月

9

日

至

3

月

16

日

1-1探討