在1-1中你已經知道了如
及
的圖形特性，現在讓我們嘗試其他型式的二次函
數，看看它們會有什麼令你驚奇的結果！
要進行這一節的內容，你必須複習以下知識與技
巧：
1.將未知數代入式子中求值的練習。
2.完全平方公式。
3.複習「配方法」。
本節希望你學會畫出如下列的二次函數的圖形，
並看出它們的的特性：
1.會畫
，並知頂點坐標。
2.會畫
，並知頂點坐標。
3.會畫
，並知頂點坐標。
4.了解如果題目，如果是型如：
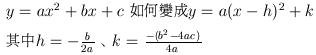
，並知頂點坐標。
１.請試著畫出以下的圖形：
對照用的圖形 y=x
、y=
- x
A. y=(x－5) B.
y=(x－10)
C. y= - (x－5)
D. y= - (x－10)
描點後得：
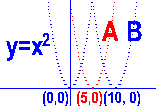
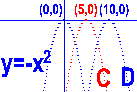
２.請試著畫出以下的圖形：
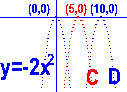
對照用的圖形 y=２x、y=
- ２x
A. y= 2(x－5) B.
y= 2(x－10)
C. y= - 2(x－5)
D. y= - 2(x－10)
描點後得：
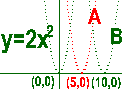
結論
1.y=x、
y=(x－5)、y=(x－10)的圖形大小均
相同，差別在位置不同：將y=x往右移動5及
10格
2.y=-x、
y=-(x－5)、y=-(x－10)的圖形大小
也相同，差別在位置不同：將y=-x往右移動
5及10格
3.同樣地,【y=2x、y=2(x－5)、y=2(x－10)】
【 y=-2x、
y=-2(x－5)、y=-2(x－10)】
兩組的差別也是位置的不同。
故可歸納得
y=(x－a)是將y=x
往右移a格
y=2(x－a)是將y=2x
往右移a格
＊＊即y=(x－a)意思是將
y=x
移a格 a>0，代表往右移a格
a<0，代表往左移a格
且頂點在(a,0)
＊＊即y=a(x－b)
是將y=ax
移b格 b>0，代表往右
b<0，代表往左
且頂點在(b,0)
【註】：請自行練習如 y=(x＋5)等類型的圖形
１).請試著畫出以下的圖形：
對照用的圖形 y=2(x-3)
A. y=2(x－3)＋
10 B. y=2(x－3)－10
(２).請試著畫出以下的圖形：
A. y=x－
6x+9【y= (x-3)】
B. y=x－
6x 【y= (x-3)-
9】
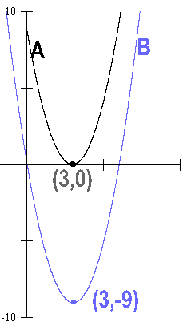
描點之後，得：
(1) 
(2) 
結論
1.y=2(x-3)
、y=2(x－3)＋
10 、y=2(x－3)－10
的圖形大小均相同，差別在位置不同：
＊＊將y=2(x-3)
往上、下移動10格
2. y=x－
6x+9、y=x－
6x 的圖形乍看之下並不
相同，但經過變型之後得：【y=
(x-3)】
【y=
(x-3)-
9】 畫出來的圖形竟是相同的，
差別只在位置不同：將y=x－
6x+9往下移動
得到y=x－
6x。
＊＊y=a(x－h)＋k意思是將
y=a(x-h)
移k格 k>0，代表往上k格
k<0，代表往下k格
且頂點在(h,k)
＊＊想畫出 y=ax＋bx 的圖形時，或想
畫出 y=ax＋bx+c 的圖形時，
有二個方法：
(1)直接描點。
(2)利用配方法變型為y=a(x-h)+k
再利用「平移」觀念，也可以畫出圖形。
【提醒】y=x－
6x怎麼配方啊？？
【作法】
y=x－
6x
=x－
6x +3-3《加上x係數一半的平方》
=(x－3)－９
《有借(＋)有還(－)喔!》
1.不確定平移的方向，例如(x－3)－９，不確定
是往左右３格，還是上下９格。
2.無法順利進行「配方法」。
3.只是記憶作法，尚不了解「頂點」的意義。
例如：畫y=－x時，已知５點坐標如下：
卻看不出來頂點是那一個。
|
1.二次函數 y=(x－3) |
|
|
2.將y=3x |
|
|
3. y=2(x+4) |
|
|
4.將y=x |
|
|
5. y=2x+12x 的頂點坐標是為何? |
解答：D、C、B、C、A
深呼吸一口氣，準備測驗10題了喔!(適用IE^_^)
3 |
月 |
9 |
日 |
至 |
3 |
月 |
16 |
日 |
|
|
|
|
|
|
