 2007.7.
2007.7.
請問:如下圖,圓中有一正△,請問D是BC弧上任一點,請問AD與CD+BD的長度比較為何?
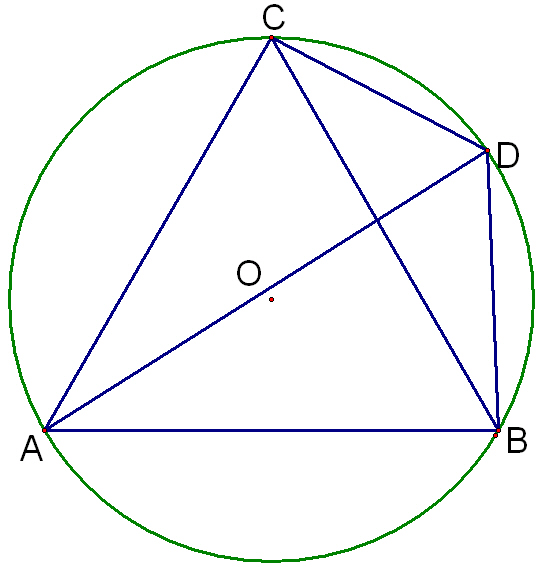
( )AD=CD+BD AD>CD+BD AD<CD+BD 無法比較
思考:
看到這個題目有圓,有正△,要比較線段長度大小,我們應該會幾個思考方向:
1.會不會是利用「全等△」?
2.會不會是利用「相似△性質」?
如果都想不出來,該怎麼辦呢?利用電腦也可以幫助我們思考解題的方向喔?
由右圖電腦的協助下,你會發現答案是
AD=CD+BD 但是 Why? →看不到JAVA的網友,請直接往下看「幾何證明」
理由是
【幾何證明】
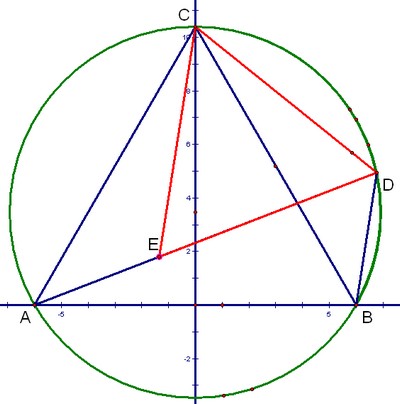 |
1.在AD上找一點E,作ED=CD,因為∠CDE=∠ABC=60° |
| 【同弧所對圓周角相等】, 故△CDE為正△。 | |
| 2.在△ACE與△BCD中,∠ACE=∠BCD,AC=BC,CE+CD | |
故△ACE全等△BCD(SAS) |
|
| 3.AD=AE+DE =BD+CD |