EditRegiFlashVideoon4　 　　 　　　　　

2007.10.12 　　　　　　　數學探奇---尋找Pattern 　　　　　　數學王子

　　很多人不喜歡數學的理由很簡單，就是對於數學題目無法掌握，因此常有「我會的題目都不考」之嘆，因此數學王和讀者們一起
來聊一聊，隱藏在數學題目背後的意義吧。

　　　Pattern(有人直譯作胚騰)，是一種隱藏在題目表面的弦外之音，換句話說就是一種模式，讀者們可以想一想，為什麼你要去買漢
堡時會想到「麥當勞」，為什麼一大群人去看棒球賽時會自動帶著「加油棒」或「相關道具」，這就是「Pattern」，舉例來說：本來我
們是沒有這種習慣的，但是我們透過觀察發現以下特性：當我們要作某些事情時，多數人都會作同樣的事，所以我們也因此跟著作，久
而久之，它成為我們的自然反應。

　　　以計算1+3+5+7+9+11+13+15之值為例，讀者心想這個題目有什麼好說的，直接計算不就好了，事實上也是如此，不過，當數目
字的個數變多時，直接計算的麻煩會愈來愈明顯，所以，我們不禁想起了數學神童--高斯「Gauss」小時候的驚人天份，老師要小高斯計
算的題目雖然不是這一題，不過其實還類似的，計算1+２+３+４+５+…+100之值。小高斯的想法是把這個題目的數字從100到1重排一
次，然後他發現上下每一組數字的和都是101，因為有50組，所以答案就是　(101×100)÷2=5050，藉由這個想法，我們也可以用它來解決
上面這個問題，1+3+5+7+9+11+13+15＝(16×8)÷2=64

　　　　　　
如上所述，同學們學完這一題之後, 並沒有任何的模式留存下來，所以題目都是獨立的，遇到寫法不同或是有些變化的類型不得不舉白旗
投降，事實這個題目還有另一種看法。
　　　【圖形觀點】
　　　　　　　　　　　　　　

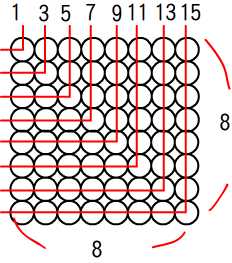
　　　　　　　　　1+3+5+7+9+11+13+15＝８=64
　　　　因此，我們可將其一般化，寫成　1+3+5+7+…＋（２K－1）＝ n　K=1,2.3....n

　　有時候不同的類似的題目也會有類似的想法，讀者在計算相似三角形的題目中也會遇到同樣的情境，如下圖，在三角形中有一組
平行線，將兩腰截出數個個等分，請問其面積比為何？換句話說，已知 DE//FG//BC，且AD:DF:FB=1:1:1，求△ADE:梯形DFGE:
梯形FBCG之面積比。讀者若依照相似形的概念，則會利用相似形之面積比為邊長的平方比這個觀念，所以可得面積比為：
　　　△ADE:△AFG:△ABC = 1:2:3
　　　　　　　　　　　　= 1 : 4: 9
　　　所以△ADE:梯形DFGE:梯形FBCG之面積比＝１：（4-1）：（9-4）
　　　　　　　　　　　　　　　　　　　　　　= 1：3：5
　　 　

事實上，我們也可以利用上一題圖示的方式來解決這個問題，而且讀者會發現它們之間的的相似度很高，因為每一個小區域的面積比
是不是很像上個題目中每一項的個數和！
　　　　　　

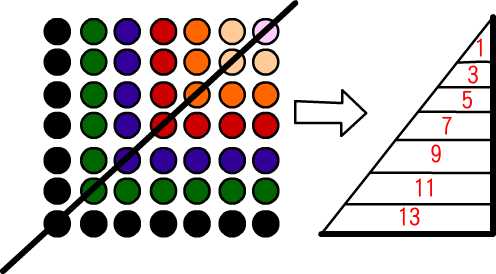
　　您瞧，我們發現它們有共同的模式了，這個就是一個Pattern，發現題目的共通性，可以讓我們更有興緻繼續挑戰下去。
　【挑戰】計算以下圖形的面積比。
　　　　

　　　　解法：
　　　　利用圖形來說明最簡潔了，請看：

　　　看完這篇介紹，讀者是不是覺得數學多了一點親近的理由，尋找Pattern是數學家們很熱衷的一件事，例如：雖然已知π無限小數
，但是數學家還是希望知道它是否會有循環？又如，質數有無限多個，但是數學家卻嘗試找尋一個可以判斷是否為質數的規律，也因為
有這些研究，數學由純粹的計算轉化為一個努力的目標，那個目標或許對一般人而言是微不足道，但是人們藉探索它帶來的喜樂，卻是不
可計量的。