 2007年8月11日
2007年8月11日
思考:
看到這個題目, 我們應該會幾個思考方向:
1.會不會是利用乘法公式?
2.會不會是利用十字交乘法?
3.會不會是利用雙十字交乘法?
作法:
【法一】由因式的概念思考,
如果題目可以因式分解,應該只有以下幾個可能:
 =(x+a)(x+b)(x+c)(x+d)
=(x+a)(x+b)(x+c)(x+d)
=(x+a)(x+b)(x +cx+d)
+cx+d)
=(x+a)(ax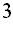 +bx
+bx +cx+d)
+cx+d)
=(x +ax+b)(x
+ax+b)(x +cx+d)
+cx+d)
以一次因式來看,展開之後比較係數可知,abcd=-2,換句話a,b, c, d必為2的因數
但是x+1,x-1,x+2,x-2 都不是 的因式。
的因式。
因此, =(x
=(x +ax+b)(x
+ax+b)(x +cx+d)
+cx+d)
=(x +ax+1)(x
+ax+1)(x +cx-2)
+cx-2)
=(x +ax-1)(x
+ax-1)(x +cx+2)
+cx+2)
1°若 =(x
=(x +ax+1)(x
+ax+1)(x +cx-2)
+cx-2)
=x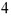 +(a+c)x
+(a+c)x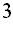 +(ac-1)x
+(ac-1)x +(c-2a)x-2
+(c-2a)x-2
比較係數得 a+c=1, ac-1=-1, c-2a=-2
a=1, c=0
故 =(x
=(x +x+1)(x
+x+1)(x -2)
-2)
2°若 =(x
=(x +ax-1)(x
+ax-1)(x +cx+2)
+cx+2)
=x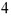 +(a+c)x
+(a+c)x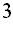 +(ac+1)x
+(ac+1)x +(2a-c)x-2
+(2a-c)x-2
比較係數得
由a+c=1, ac+1=-1, 可解出a=-1,c=2或a=2,c=-1
但代入2a-c=-2 均不合,故此式不成立。
【法二】直接作因式分解----拆項法
 =x
=x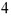 +x
+x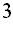 +x
+x -2x
-2x -2x-2
-2x-2
=x (x
(x +x+1)-2(x
+x+1)-2(x +x+1)
+x+1)
=(x +x+1)(x
+x+1)(x -2)
-2)